- Innovaciones
- Artículos sobre la aplicación de PCI
- Trading de Portfolios
Optimización del Portafolio a través del Método PQM (Parte 1)
La búsqueda de una estructura optima de acciones en un portfolio, por supuesto que no es una tarea sencilla. Por un lado, mucho depende de los parámetros de las acciones incluidas en las carteras, y por otra parte, sobre las preferencias y restricciones individuales del inversionista. Sin embargo, la teoría financiera moderna, y los nuevos métodos de análisis y negociación, simplifican considerablemente el proceso.
El Método GeWorko puede servir como un ejemplo de implementación de la teoría moderna del Portfolio, la cual permite construir y analizar numerosas variantes de Portfolios, creada a partir de una amplia gama de acciones. Y el valor de las capacidades de análisis, radica en no solo siguiendo los cambios absolutos de precios en los Portfolios, sino también en el estudio del comportamiento del portfolio en relación a todo el mercado o, por ejemplo, a un portfolio alternativo, que permite tomar decisiones de inversión de una manera oportuna. El resultado del método dispositivo viene a ser la creación de una nueva unidad financiera – instrumento compuesto (PCI – personal composite instrument).
En este articulo nos centraremos en un conjunto de 6 acciones estadounidenses, que ha primera vista han arrojado resultados relativamente positivos, en los últimos años. A través del Método GeWorko hemos construido un Portfolio con un crecimiento considerable en el periodo post-crisis. Nuestra selección (con pesos aleatorios correspondientes) se compone de:
- Walt Disney Company (DIS – 20%)
- Home Depot Inc. (HD – 20%)
- Honeywell International Inc. (HON – 15%)
- International Business Machines Corporation (IBM – 15%)
- Coca-Cola Company (KO – 10%)
- McDonald’s Corporation (MCD – 20%)
Al comprar la dinámica del Portfolio con el mercado (El Índice promedio Dow Jones Industrial condicionalmente representa el mercado e incluye todas las acciones cotizadas), resultó que el Portfolio ha sido sistemáticamente superando el índice antes de la crisis, durante la crisis y en el periodo de recuperación. El grafico PCI, formado en unos pocos segundos, ilustra con éxitos el comportamiento del Portfolio en relación con el índice:
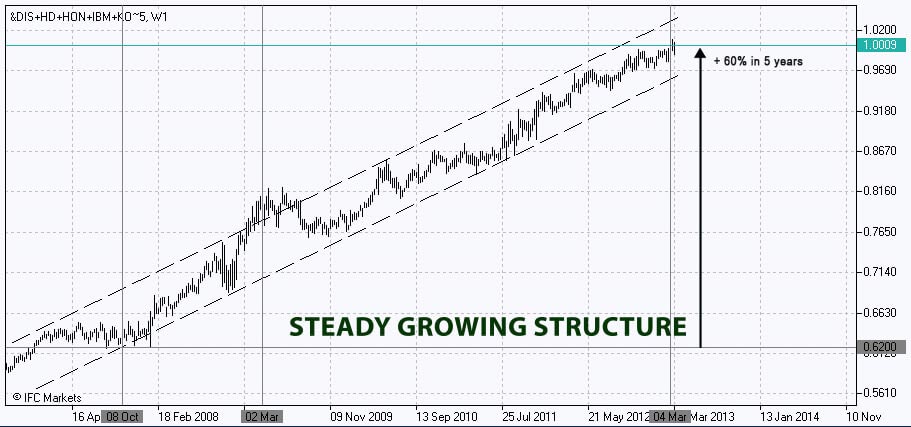
A pesar de la selección exitosa y aleatoria de los pesos del Portfolio, aun no sabemos si es del todo optima, es decir, si existen otros coeficientes de peso allí, proporcionando menor riesgo en el mismo nivel de rendimiento, o bien un mayor retorno en el mismo niel de riesgo. Si logramos encontrar un Portfolio más preferible para un inversor racional, este sin duda seria un Portfolio con coeficientes de pesos aleatorios. Sin embargo, la determinación de la optimalizad del portfolio para un inversor, como ya se ha mencionado anteriormente, dependerá de las preferencias y restricciones individuales. Sin requisitos concretos para el perfil de riesgo-retorno del Portfolio, no podemos saber si, por ejemplo, es más preferible un Portfolio con un alto riesgo de retorno pero también con un alto nivel de riesgo, es más preferible para un inversor que el primero. En este sentido para los propósitos analíticos, se considera como Portfolio optimo al que tenga el máximo rendimiento por unidad de riesgo. Este Índice se conoce como el ratio de Sharpe.
En contraste de su versión tradicional, que muestra la relación de la prima de riesgo por encima a la tasa sin riesgos de desviación estándar, vamos a maximizar la relación de rendimientos del Portfolio volviendo al Portfolio de desviación estándar, sin ajustar la tasa libre de riesgo. Esa simplificación de ninguna manera va a influir en las conclusiones, lo que permitirá la comparación de las eficacias de los Portfolios alternativos de inversión. Primero, volvamos al Portfolio principal con pesos dados al azar y determinar sus parámetros de riesgo y rentabilidad. El análisis del Portfolio en los datos mensuales de los precios de cierre de seis stocks, sobre la muestra de Enero 2005- Abril 2013. Dado que el objetivo inicial fue el de comparar la dinámica del Portfolio con el índice (el mercado), hemos decidido aplicar un enfoque ligero y no estándar, para ajustar los precios de cierre mensual del Stock, dividiéndolos por los valores de índices correspondientes. Sobre la base de los rendimientos logarítmicos, hemos calculado medios devueltos y desviaciones estándares devueltas de 6 hileras de datos. Los resultados del cálculo se presentan en la tabla siguiente:
| DIS | HD | HON | IBM | KO | MCD | |
| Mean Return | 0.49% | 0.24% | 0.40% | 0.42% | 0.35% | 0.77% |
| StDev | 4.25% | 5.73% | 4.51% | 4.53% | 3.95% | 4.09% |
| Sharpe Ratio | 0.11 | 0.04 | 0.09 | 0.09 | 0.09 | 0.19 |
Resulto que la mayor (0,77%) rentabilidad media mensual (en comparación con el índice), se ha mostrado por los Stocks MCD, los mas pequeños- por los Stock HD (0,24%). La desviación estándar mas pequeña se ha mostrado por el Stock KO (3,95%), la más grande, por los Stock HD (5,73%). Además, se ha calculado la versión simplificada de la ratio de Sharpe, que muestra la relación de retorno de acciones de riesgo. Los Stocks MCD tienen el coeficiente mas alto (0,19), mostrando la mejor relación de rendimiento por unidad de riesgo. Este hecho nos permite suponer que se trata de acciones MCD que mostraran el coeficiente de ponderación más alto en un Protfolio "optimo". Para continuar con el análisis, también necesitan saber cómo las acciones están relacionadas entre sí,- se utilizan los coeficientes de covarianza.
Teniendo todos los paramentaros de entrada necesarios y suponiendo que los valores de retorno obtenidos y de desviación estándar por seis Stocks, son las mejores estimaciones de rendimientos y riesgos esperados, podemos empezar formando Portfolios. Recuerde que los datos de entrada ya han sido ajustados por el valor del índice. Es por ello que los Portfolios que debemos obtener, ya reflejaran el comportamiento en relación al mercado.
El primer Portfolio (P1) se convertirá en el punto de partida para la búsqueda de combinaciones mas exitosas de acciones. Es el Portfolio con coeficientes de peso aleatorio, su grafico de precios se ha presentado tempranamente. Conociendo el riesgo y parámetros de retorno de seis acciones, incluidas en el Portfolio, su peso, y la matriz de covarianza se pueden calcular, la rentabilidad media mensual del Portfolio y su desviación estándar. Es fácil darse cuenta de que por medio de activos combinados, hemos logrado una reducción significativa de riesgo. La desviación estándar del Portfolio P! es de solo 1, 74% y la rentabilidad es -0,46% :
| DIS | HD | HON | IBM | KO | MCD | P1 | |
| Mean Return | 0.49% | 0.24% | 0.40% | 0.42% | 0.35% | 0.77% | 0.46% |
| StDev | 4.25% | 5.73% | 4.51% | 4.53% | 3.95% | 4.09% | 1.74% |
| Sharpe Ratio | 0.11 | 0.04 | 0.09 | 0.09 | 0.09 | 0.19 | 0.26 |
Además, en comparación con cualquiera de las seis acciones, el Portfolio tiene mayor rendimiento por unidad de riesgo, la evidencia de que la relación de esta, es la proporción Sharpe (0,26%), la cual últimamente determina la efectividad del Portfolio.
Ahora conociendo las características del Portfolio , podemos iniciar la búsqueda de una combinación de acciones tal, que mejor corresponderán a nuestras preferencias y restricciones. Como ya se ha mencionado, se ha elegido el ratio de Sharpe como criterio básico de optimización. Cambiando los pesos de los seis Stocks que forman el Portfolio, debemos buscar una combinación tal, que corresponda a la proporción más alta posible de retorno de riesgo. Las únicas condiciones de optimización que establecimos, es que los coeficientes de peso deben ser inferiores a cero, y su suma debe ser igual al 100%, a fin de mantener la oportunidad de comparar los Portfolios.
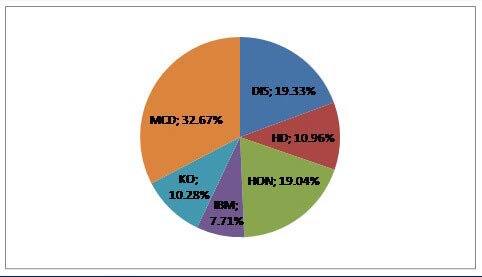
La solución nos lleva a la siguiente composición de Portfolios: Como hemos esperado, las acciones MCD tienen el mayor peso (32,67%), ya que tenían el mayor ratio de Sharpe. Luego vienen las siguientes acciones en orden decreciente de peso: DIS (19,33%), HON (19, 04%), HD (10,96%), KO (10,28%) e IBM (7,71%):
Como resultado de ellos, el portfolio (P2), obtenido mediante el cambio de los pesos para maximizar el ratio de Sharpe, mostro claramente un mejor rendimiento que el Portfolio con coeficientes de ponderación al azar (P1):
| DIS | HD | HON | IBM | KO | MCD | P1 | P2 | |
| Mean Return | 0.49% | 0.24% | 0.40% | 0.42% | 0.35% | 0.77% | 0.46% | 0.52% |
| StDev | 4.25% | 5.73% | 4.51% | 4.53% | 3.95% | 4.09% | 1.74% | 1.72% |
| Sharpe Ratio | 0.11 | 0.04 | 0.09 | 0.09 | 0.09 | 0.19 | 0.26 | 0.30 |
El ratio de Sharpe maximizado fue de 0,3 para P2. Este valor es superior que el ratio de P! (0,26%) y para las acciones individuales. Por otra parte, tanto la rentabilidad (0,52%) y la desviación estándar (1,72%) parámetros son estrictamente mejores. La conclusión es que el Portfolio formado por la maximización del ratio de Sharpe, siempre es mas preferible para un inversor racional (recordemos nuestra hipótesis de que el análisis de los riesgos tomados y devoluciones son su mejor estimación).
Con el modulo PCI podemos construir el Portfolio "opimo", introduciendo los coeficientes de ponderación obtenidos para seis Stocks en el presupuesto y fijación de precios en contra de un Portfolio con un valor similar, que consiste en el índice Dow Jones. (Ver el grafico).
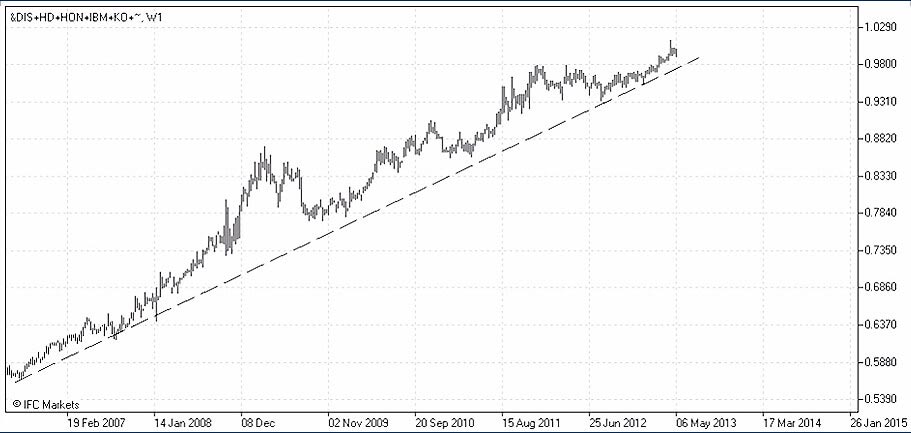
Al igual que en el caso anterior con el aleatorio Portfolio P1, obtenemos una estructura en constante crecimiento en los últimos 7 años, con una volatilidad aumentando considerablemente en tiempos de turbulencia económica.
Sin Embargo, hacemos hincapié en que el portfolio optimo es solo para nosotros, ya que hemos seleccionado el ratio de Sharpe como criterio básico de optimización. Solo podemos confirmar que con los parámetros de entrada existentes no hay otro Portfolio que nos permitirá alcanzar una mayor rentabilidad (>0,52%) para un nivel de riesgo determinado (1,72%) y también que no Portfolio menos riesgoso (1,72%) para la rentabilidad dada (0,52%). Sin embargo, es posible que un inversor esté listo y posea capacidades objetivas para aceptar un riesgo más alto, a fin de lograr un nivel de rendimiento mas alto o simplemente por el contrario, el inversor busque obtener el riesgo del Portfolio más bajo posible.
Seguir leyendo en "Estructura de Optimización de Portfolios a través del Metodo GeWorko (parte 2)"
Artículos previos
- El cuarto postulado de la Teoría de Dow: sirviendo al inversor
- Spread de portafolio a base de futuros continuos
- Portfolio de Sharpe – "Tres Líderes"
- El Método de Cotización del Portafolio para el Análisis de Portafolios "buenos" y "malos"
- Optimización del Portfolio a través del Método PQM (Parte 2)
- Construcción y Análisis de Portafolios de Acciones con el Método de Cotización del Portafolio PQM
